整理.撰文 經理人編輯部
什麼是賽局理論、奈許均衡?想贏過競爭對手,你該瞭解的經濟學理論
秦末群雄並起,初掌楚軍兵權的項羽奉命領 5 萬軍,馳赴被秦軍包圍的鉅鹿城救援。面對 30 萬秦軍,項羽渡黃河後,下令將所有船鑿沉,鍋釜也全部打破,讓全營士兵抱著必死的決心作戰。秦將王黎嘲笑項羽,連兵法都不懂,打仗豈能不留後路?沒有想到,楚軍竟以一當十,九戰九捷,大敗秦軍。
項羽是自信於楚軍勇猛嗎?恐怕不是,而是項羽了解,5 萬對 30 萬,對方將領只要採取正規戰,失敗的可能性極小,換句話說,想要求勝,只能出其不意。 所以他自斷後路,示敵以弱,讓對手掉以輕心。這種 預測局勢得失,布局以牽制對手,進而求勝的思考方式,近似於經濟學中的「賽局理論」。
賽局模型:囚徒困境
賽局理論最有名的例子,就是普林斯頓大學數學教授阿爾伯特.塔克(Albert Tucker)講解的「囚犯困境」(Prisoner’s Dilemma)。假設警察抓到兩名搶銀行的嫌犯,卻苦無證據定罪。警察將兩人分開囚禁,並分別跟他們說:「如果你不認罪,另一個人認罪,那他會無罪釋放,你唯一死刑。」此案中,嫌犯都清楚,如果彼此都不認罪,頂多證據不足關 1 年。然而,兩位嫌犯都害怕對方會招認,所以寧願選擇認罪。
囚犯困境的例子中,雖然沈默不認罪對雙方最有利(各判 1 年),但兩名犯人會因為害怕對方自白會加重自己的刑期,所以最後都會認罪(各判 15 年),這個賽局就成了「困境」。
囚徒困境能解釋商場上的「削價競爭」,競爭廠商壓低價格,你不得不跟進,但跟進對雙方都沒好處。學習這個觀念,最大的收穫在於,我們必須了解, 個人的最佳選擇,有時候並非是整體最佳解,有賽局的觀念,就會先考量對手想法。
賽局模型:零和賽局
零和賽局是在賽局理論中,出現「非合作博弈」的情況,只會有一個人贏、另一個人輸,兩個人的利益總和相加等於零,故稱零和賽局。這個思考策略經常運用在運動比賽,猜測對手戰術。通常,一個人的選擇,會被另一個人影響,沒有任何選擇具有絕對的優勢,亦即沒有辦法確保自己一定會贏。
剪刀石頭布是零和遊戲最常見的例子,以小李、小張兩人猜拳來說,贏的 + 1 分、平手 0 分、輸的 - 1 分,兩人成績加總永遠為零。即便兩人都沒有優勢,還是有跡可循。比方說,小李連續 5 次都出「布」,小張觀察到這點,改出剪刀的勝率就會提高。《理性》一書建議, 在零和賽局裡,理智者反而應該要保持隨機性,使對手難以預測自己的行動路線。
奈許均衡:單獨一方改變策略時,無法提高報酬
在前 2 個賽局理論的例子中,犯人決定要不要認罪,屬於「主觀」判斷的賽局;隨機出拳的剪刀、石頭、布,長期下來,每種拳出現的機率為 1/3,這種賽局的策略接近「客觀」機率。
當賽局裡這兩種狀況都有可能出現時,就稱為混和策略。1994 年諾貝爾經濟學獎得主約翰.奈許(John Nash)證明了:「如果允許混合策略,則參賽者與策略數目有限的任何不合作賽局,都一定會有奈許均衡存在。」
奈許均衡(Nash Equilibrium),也叫非合作均衡。意思是,在賽局中達到某種平衡狀態,且所有參與者都能接受結果,就是奈許均衡。舉例來說,在討價還價後,賣家與消費者都達成對某件衣服價格的共識。更重要的是, 在這場賽局的所有參與者都相信,只要某一方單獨改變策略,都會使結果變得不好。
以企業的薪資策略為例,如果不提高薪資,員工可能會跳槽;提高薪資,可以留才、挖角。但如果整個業界裡,沒有企業率先提高自己的薪資水準,員工就沒有跳槽動機,因此常見的情況是,有可能整個產業薪資都沒有起色,保持了奈許均衡;另一種情況是,產業處於上風期,領頭企業加薪了,其他企業也會跟進加薪,避免人才流失,同樣達到奈許均衡。
賽局的演進:考量行動順序、資訊透明程度
子賽局完美均衡
奈許均衡是建立在參與者同時行動的前提上,也就是靜態賽局。但現實社會中,不論企業或個人決策都有先後之分。另一方面,奈許均衡不一定只有一個。
比如《玩命關頭 7》中,唐老大與戴克蕭開車互撞。最好的情況是一個活著,另一個死亡,這就得賭誰先膽小偏移車道,所以奈許均衡有兩個:唐老大先偏移,戴克蕭直衝;唐老大直衝,戴克蕭先偏移,參賽者難以預測結果。
為了解決這兩個問題,同樣在 1994 年獲頒諾貝爾經濟學獎的賴因哈德.澤爾騰(Reinhard Selten)為賽局引入動態的概念,提出「子賽局完美均衡」(SPNE,Subgame Perfect Nash Equilibrium),也就是思考如果讓對手先採取行動,自己應該如何因應;和如果自己先下一步棋,對手可能會採取什麼行動,統籌所有子賽局的可能性之後再做決策。
舉例來說,有家新百貨公司準備進入某市場,舊百貨公司可以選擇維持原價或降價。
此時,第一個子賽局,是舊公司觀察到新公司進入市場後的賽局;第二個子賽局,是舊公司觀察到新公司不進入市場後的賽局。從各個子賽局的結果,回推舊公司的最適策略。
貝氏奈許均衡
同時,賽局理論原先假設資訊完全透明,跟現實世界的情況不盡相符。所以,1994 年另一位諾貝爾經濟學獎的約翰.海薩尼(John Harsanyi)為了分析不完全訊息之下的非合作賽局理論,提出「貝氏奈許均衡(Bayesian-Nash equilibrium)」。
舉例來說,B 企業考慮進入 A 企業獨佔的某市場。B 企業知道,A 企業是否會阻擾他進入,取決於阻擾所花費的成本:如果成本高,A 就不會阻擾;如果成本低,A 就會阻擾。然而,A 企業的阻擾成本是多少,B 企業卻不知道。
這種 A 方知道,B 方卻不知道的資訊,在海薩尼的非合作賽局中被稱為類型(types)。A、B 企業都知道自己的類型(成本高、成本低),不知道另一方的類型,但卻能得知類型的分佈,如阻擾成本高的機率是 60%、阻擾成本低的機率是 40%。
貝氏奈許均衡中,參賽者只知道自己的類型,不知道其他人的類型,但所有人都知道類型的分佈。所以,參賽者只能依照自己的類型,與類型的分布,找出利益最大化的決策。
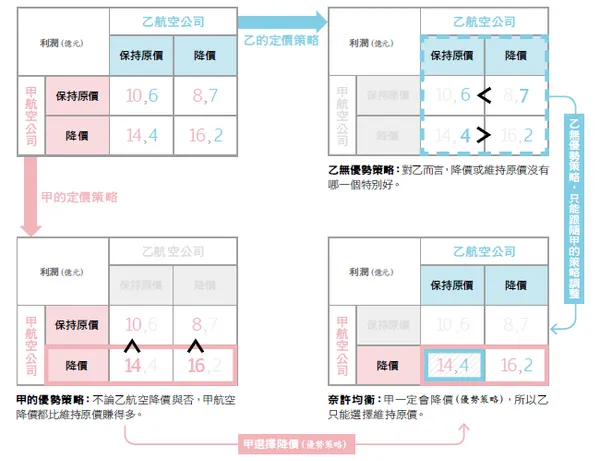
從定價策略學賽局理論:優勢策略與奈許均衡
甲、乙兩家相互競爭的航空公司,在上圖標示出兩方選擇原價策略和降價策略後的結果。在決定票價前,企業應該要先探索自己有無「優勢策略」。
以下拆解成 3 張圖來做解讀:
當甲、乙都採原價時,甲的利潤有 10 億,乙的利潤有 6 億。但假如甲航空公司通過計算後發現,無論自己降價後因為搶奪乙的市占率,無論乙有沒有降價,都可以得到更多的利潤,因此甲一定會降價。
乙航空公司完全沒有優勢,降價或維持原價可獲得的利潤,要看甲航空公司的價格策略而定。
因此在甲航空公司選擇降價後,乙航空公司只能依此選擇維持原價。
想更瞭解賽局?推薦兩本書
1.《賽局高手》,巫和懋、夏珍著,時報出版
作者巫和懋,中歐國際工商學院經濟學教授,過去在台大開設「賽局與產業競爭策略」屢次被評為學生最受歡迎課程。在本書中,他從賽局的誕生、談到靜態、動態賽局,由淺入深並輔以產業與政治的案例,適合想了解賽局的讀者。
2.《微觀動機與宏觀行為》,湯瑪斯.謝林(Thomas Schelling)著,臉譜出版
本書介紹人的決策,除了受理性控制外,尚會被其他人的行為所影響。結果導致有些個人、組織能順利合作,有些卻彼此衝突。











